Linear Algebra: Dot Product, Vector Length, Angles Between Vectors

Linear Algebra: Vector Dot Product

The dot product operation is a way to multiply a vector by another vector. Dot product notation is, not surprisingly, just a $\cdot$ between two vectors: $\overrightarrow{a}\cdot \overrightarrow{b}$. ($\times$ between vectors is the cross product, a different vector multiplication). The dot product is defined as $\overrightarrow{a}\cdot \overrightarrow{b}=\left(a_1,a_2,\dots <!--FUNCTION\; APPLICATION-->,a_n\right)\cdot \left(b_1,b_2,\dots <!--FUNCTION\; APPLICATION-->,b_n\right)=a_1\ast b_1+a_2\ast b_2+\cdots +a_n\ast b_n$. The dot product takes two vectors, and generates just a number. For example, $\left(1,3\right)\cdot \left(4,7\right)=1\ast 4+3\ast 7=4+21=25$.

Dot Product Relation to Vector Length

To find the length of a vector in 2 dimensions, we just need to take the square root of its components squared. This is just the Pythagorean theorem. For example, $\overrightarrow{a}=\left(3,4\right)$, then its length denoted with double lines is $\left|\right|\overrightarrow{a}\left|\right|=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$. We can generalize this notion of length to any number of dimensions by adding additional vector terms to the sum under the sqrt. Generalized Pythagorean theorem: $\left|\right|\overrightarrow{v}\left|\right|=\sqrt{v_1^2+v_2^2+\cdots +v_n^2}$. Notice that a vector ”dotted” with itself, will get all the terms of the vector squared. So, to get the length using the dot product, we just need to take the square root of the vector ”dotted” with itself. $\left|\right|\overrightarrow{v}\left|\right|=\sqrt{\overrightarrow{v}\cdot \overrightarrow{v}}$.

Cauchy-Schwarz Inequality

The Cauchy-Schwarz Inequality relates vector dot products to vector magnitudes, and generalizes to any number of dimensions. The inequality states that the absolute values of the dot product of two vectors is less than the value of their lengths multiplied: $|\overrightarrow{a}\cdot \overrightarrow{b}|\le \left|\right|\overrightarrow{a}\left|\right|\ast \left|\right|\overrightarrow{b}\left|\right|$ where $\overrightarrow{a},\overrightarrow{b}\in {ℝ}^n\wedge \overrightarrow{a},\overrightarrow{b}\ne \overrightarrow{0}$. The two vectors are only equal when they are colinear: $|\overrightarrow{a}\cdot \overrightarrow{b}|=\left|\right|\overrightarrow{a}\ast \overrightarrow{b}\left|\right|\iff \exists <!--FUNCTION\; APPLICATION-->\left(c\in ℝ\right)\text{ for }\overrightarrow{a}=c\ast \overrightarrow{b}$.

$$p\left(t\right)=\overrightarrow{v}=\left|\right|t\overrightarrow{a}-\overrightarrow{b}|{|}^2\ge 0\text{ because }|\left|\overrightarrow{v}\right||=\sqrt{components>=0}$$

$$\left|\right|\overrightarrow{v}|{|}^2=\overrightarrow{v}\cdot \overrightarrow{v}$$

$$\left(t\overrightarrow{a}-\overrightarrow{b}\right)\cdot \left(t\overrightarrow{a}-\overrightarrow{b}\right)$$

$$\text{ Dot product is distributive, communative, and associative}$$

$$t\overrightarrow{a}\cdot t\overrightarrow{a}-\overrightarrow{b}\cdot t\overrightarrow{a}-\overrightarrow{b}\cdot t\overrightarrow{a}+-\overrightarrow{b}\cdot -\overrightarrow{b}$$

$$\left(\overrightarrow{a}\cdot \overrightarrow{a}\right)t^2-2\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)t+\overrightarrow{b}\cdot \overrightarrow{b}\ge 0$$

$$x=\overrightarrow{a}\cdot \overrightarrow{a},y=2\left(\overrightarrow{a}\cdot \overrightarrow{b}\right),z=\overrightarrow{b}\cdot \overrightarrow{b}$$

$$p\left(t\right)=x{t}^2-yt+z\ge 0$$

$$p\left(\frac{y}{2x}\right)=x\frac{y^2}{4x^2}-\frac{y^2}{2x}+z\ge 0$$

$$\frac{y^2}{4x}-\frac{y^2}{2x}+z\ge 0$$

$$\frac{y^2}{4x}-\frac{2y^2}{4x}+z\ge 0$$

$$-\frac{y^2}{4x}+z\ge 0$$

$$z\ge \frac{y^2}{4x}$$

$$4xz\ge y^2$$

$$4\left(\overrightarrow{a}\cdot \overrightarrow{a}\cdot \overrightarrow{b}\cdot \overrightarrow{b}\right)\ge {\left(2\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)\right)}^2$$

$$4\left(\left|\right|\overrightarrow{a}|{|}^2\ast |\left|\overrightarrow{b}\right|{|}^2\right)\ge 4{\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)}^2$$

$$\left|\right|\overrightarrow{a}|{|}^2\ast |\left|\overrightarrow{b}\right|{|}^2\ge {\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)}^2$$

$$\left|\right|\overrightarrow{a}\left|\right|\ast \left|\right|\overrightarrow{b}\left|\right|\ge |\overrightarrow{a}\cdot \overrightarrow{b}|$$

Triangle Inequality

We can use the Cauchy-Schwarz Inequality to define a triangle inequality using any 2 vectors in any number of dimensions. The Triangle Inequality states that the sum of two sides of a triangle must be greater than or equal to the length of the third side. $z\le x+y$, only equal when talking about a line. We can expand this definition to vectors with $\left|\right|x+y\left|\right|\le \left|\right|x\left|\right|+\left|\right|y\left|\right|$, where they are only equal when the vectors are colinear.

$$\left|\right|x+y|{|}^2=\left(x+y\right)\cdot \left(x+y\right)$$

$$\left(x+y\right)\cdot \left(x+y\right)=x\cdot x+x\cdot y+x\cdot y+y\cdot y$$

$$\text{ Recall: }x\cdot x=\left|\right|x|{|}^2$$

$$\text{ Becomes: }\left|\right|x|{|}^2+2x\cdot y+|\left|y\right|{|}^2$$

$$\text{ We know from Cauchy-Schwarz: }x\cdot y\le |x\cdot y|\le \left|\right|x\left|\right|\left|\right|y\left|\right|$$

$$\left|\right|x|{|}^2+2x\cdot y+|\left|y\right|{|}^2\le \left|\right|x|{|}^2+2|\left|x\right|\left|\right|\left|y\right||+|\left|y\right|{|}^2$$

$$\left|\right|x+y|{|}^2\le |\left|x\right|{|}^2+2\left|\right|x\left|\right|\left|\right|y\left|\right|+\left|\right|y|{|}^2$$

$$\left|\right|x+y|{|}^2\le {\left(\left|\right|x\left|\right|+\left|\right|y\left|\right|\right)}^2$$

$$\left|\right|x+y\left|\right|\le \left|\right|x\left|\right|+\left|\right|y\left|\right|$$

Visually, if we take (1,3) and (3,4) we can create a triangle from their sum.

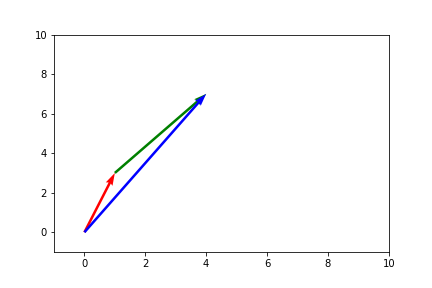
Or a line if the two vectors are colinear (drawn parallel to show better).

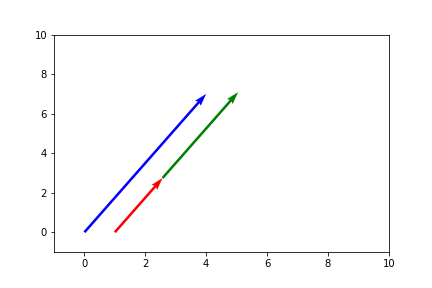
Angle Between Vectors, Perpendicularity, Orthogonality

We’ve defined the triangle inequality in any number of dimensions, and the payoff is that we can then define angles between vectors in any number of dimsensions. Let’s define a triangle with lengths $\left|\right|\overrightarrow{a}\left|\right|,\left|\right|\overrightarrow{b}\left|\right|,\left|\right|\overrightarrow{a}-\overrightarrow{b}\left|\right|$ and see if we can define angles between vectors using the triangle inequality and Law of Cosines $c^2=a^2+b^2-2ab\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$.

$$\text{ Recall Triangle Inequality: }\left|\right|x+y\left|\right|\le \left|\right|x\left|\right|+\left|\right|y\left|\right|$$

$$\left|\right|\overrightarrow{a}\left|\right|=\left|\right|\overrightarrow{b}+\left(\overrightarrow{a}-\overrightarrow{b}\right)<=\left|\right|vecb\left|\right|+\left|\right|\overrightarrow{a}-\overrightarrow{b}\left|\right|$$

$$\left|\right|\overrightarrow{b}\left|\right|=\left|\right|\overrightarrow{a}+\left(\overrightarrow{b}-\overrightarrow{a}\right)<=\left|\right|veca\left|\right|+\left|\right|\overrightarrow{b}-\overrightarrow{a}\left|\right|$$

$$\text{ Sidebar: }\left|\right|\overrightarrow{b}-\overrightarrow{a}\left|\right|=\left|\right|-1\overrightarrow{a}-\overrightarrow{b}\left|\right|$$

$$\left|\right|\overrightarrow{a}-\overrightarrow{b}\left|\right|=\left|\right|\overrightarrow{a}+\left(-\overrightarrow{b}\right)\left|\right|<=\left|\right|\overrightarrow{a}\left|\right|+\left|\right|-\overrightarrow{b}\left|\right|=\left|\right|a\left|\right|+\left|\right|b\left|\right|$$

$$\text{ Recall Law of Cosines: }{c}^2=a^2+b^2-2ab\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$$

$$\left|\right|\overrightarrow{a}-\overrightarrow{b}|{|}^2=|\left|\overrightarrow{b}\right|{|}^2+\left|\right|\overrightarrow{a}|{|}^2-2|\left|\overrightarrow{a}\right|\left|\right|\left|\overrightarrow{b}\right||\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$$

$$\left(\overrightarrow{a}-\overrightarrow{b}\right)\cdot \left(\overrightarrow{a}-\overrightarrow{b}\right)=\left|\right|\overrightarrow{b}|{|}^2+|\left|\overrightarrow{a}\right|{|}^2-2\left|\right|\overrightarrow{a}\left|\right|\left|\right|\overrightarrow{b}\left|\right|\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$$

$$\overrightarrow{a}\cdot \overrightarrow{a}-2\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{b}\cdot \overrightarrow{b}=\left|\right|\overrightarrow{b}|{|}^2+|\left|\overrightarrow{a}\right|{|}^2-2\left|\right|\overrightarrow{a}\left|\right|\left|\right|\overrightarrow{b}\left|\right|\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$$

$$\left|\right|\overrightarrow{a}|{|}^2-2\overrightarrow{a}\cdot \overrightarrow{b}+|\left|\overrightarrow{b}\right|{|}^2=\left|\right|\overrightarrow{b}|{|}^2+|\left|\overrightarrow{a}\right|{|}^2-2\left|\right|\overrightarrow{a}\left|\right|\left|\right|\overrightarrow{b}\left|\right|\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$$

$$\overrightarrow{a}\cdot \overrightarrow{b}=\left|\right|\overrightarrow{a}\left|\right|\left|\right|\overrightarrow{b}\left|\right|\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$$

Angles between vectors of any dimension are defined by $\overrightarrow{a}\cdot \overrightarrow{b}=\left|\right|\overrightarrow{a}\left|\right|\left|\right|\overrightarrow{b}\left|\right|\cos <!--FUNCTION\; APPLICATION-->\left(𝜃\right)$. Vectors are perpendicular if the angle between them is 90 degrees, and orthoginal if their dot product is $\overrightarrow{0}$. Orthonormal means two vectors’ dot product is $\overrightarrow{0}$ and each of their magnitudes is 1.