Linear Algebra: Vector Addition & Scaling

Linear Algebra: Vector Addition and Scaling

Vector Addition Definition

Vector addition is simply adding two vectors together to generate a third vector. For example, $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{c}$ if we say $\overrightarrow{a}=\left(a_1,a_2,\dots <!--FUNCTION\; APPLICATION-->,a_n\right),\overrightarrow{b}=\left(b_1,b_2,\dots <!--FUNCTION\; APPLICATION-->,b_n\right)$ then $\overrightarrow{a}+\overrightarrow{b}=\left(a_1+b_1,a_2+b_2,\dots <!--FUNCTION\; APPLICATION-->,a_n+b_n\right)$.

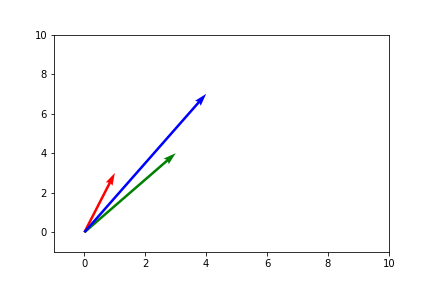
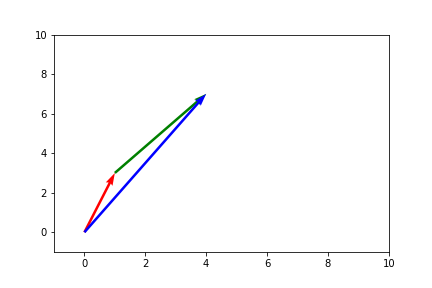
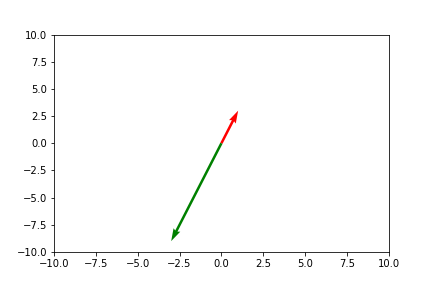
Vector Addition Visually

Vector addition can be visualed in 2-d space using the head-to-tail technique. Head-to-tail is simply putting the tail of the second vector on the head of the first vector. Let’s say we have $\overrightarrow{a}=\left(1,3\right),\overrightarrow{b}=\left(3,4\right)$. We know that the resulting vector is $\left(1+3,3+4\right)=\left(4,7\right)$.

---

(a) (1 + 3, 3 + 4) = (4, 7)

(b) (1 + 3, 3 + 4) = (4, 7) Head to Tail

---

Vector Scaling

Vector scaling is multiplying a vector $\overrightarrow{v}$ by a constant $c$ to get a vector scaled with $c$. Scaling can be done for a vector of any number of dimensions. If we have $\overrightarrow{v}$ and constant $c$, then $\overrightarrow{v}\ast c=\left(v_1\ast c,v_2\ast c,\dots <!--FUNCTION\; APPLICATION-->,v_n\ast c\right)$.

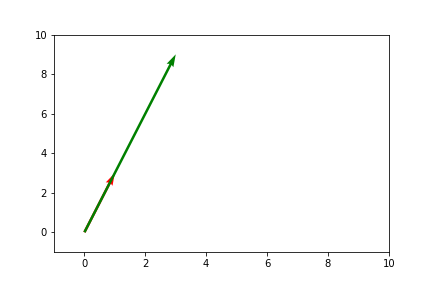
Vector Scaling Visually

Visually, vector scaling will result in a larger or smaller vector pointing in the same direction if multiplied by a positive $c$, or a larger or smaller vector pointing in the opposite direction if multiplied by a negative $c$.

---

(a) (1,3)

(b) (1,3) * 3 = (3,9)

(c) (1,3) * -3 = (-3,-9)

---